Generamos
Soluciones Tecnológicas
para Pymes
ALCHEMYLAB
Soluciones Tecnológicas
¿Alguna vez te has preguntado cómo es que herramientas como ChatGPT o los asistentes de imagen pueden "entender" lo que les pides? Detrás de estas maravillas de la Inteligencia Artificial hay un concepto clave: las redes neuronales. Su nombre no es casualidad, y en esta guía, desglosaremos cómo funcionan, comenzando por una fascinante comparación con nuestro propio cerebro.
Al escuchar "red neuronal", es normal imaginar un cerebro robótico con cables que imitan a las neuronas. Sin embargo, la realidad, aunque inspirada en la biología, es mucho más abstracta y se basa en matemáticas.
¿Por qué "neuronal"? La inspiración biológica
Para entender la neurona artificial, primero veamos la biológica. Una neurona en nuestro cerebro tiene tres partes principales:
- Dendritas: Son como antenas receptoras. Su trabajo es recibir señales de otras neuronas.
- Soma o Cuerpo Celular: Es el centro de procesamiento. Aquí se integran todas las señales y se decide si la neurona debe "dispararse".
- Axón: Actúa como un cable transmisor, llevando la señal de salida a otras neuronas.
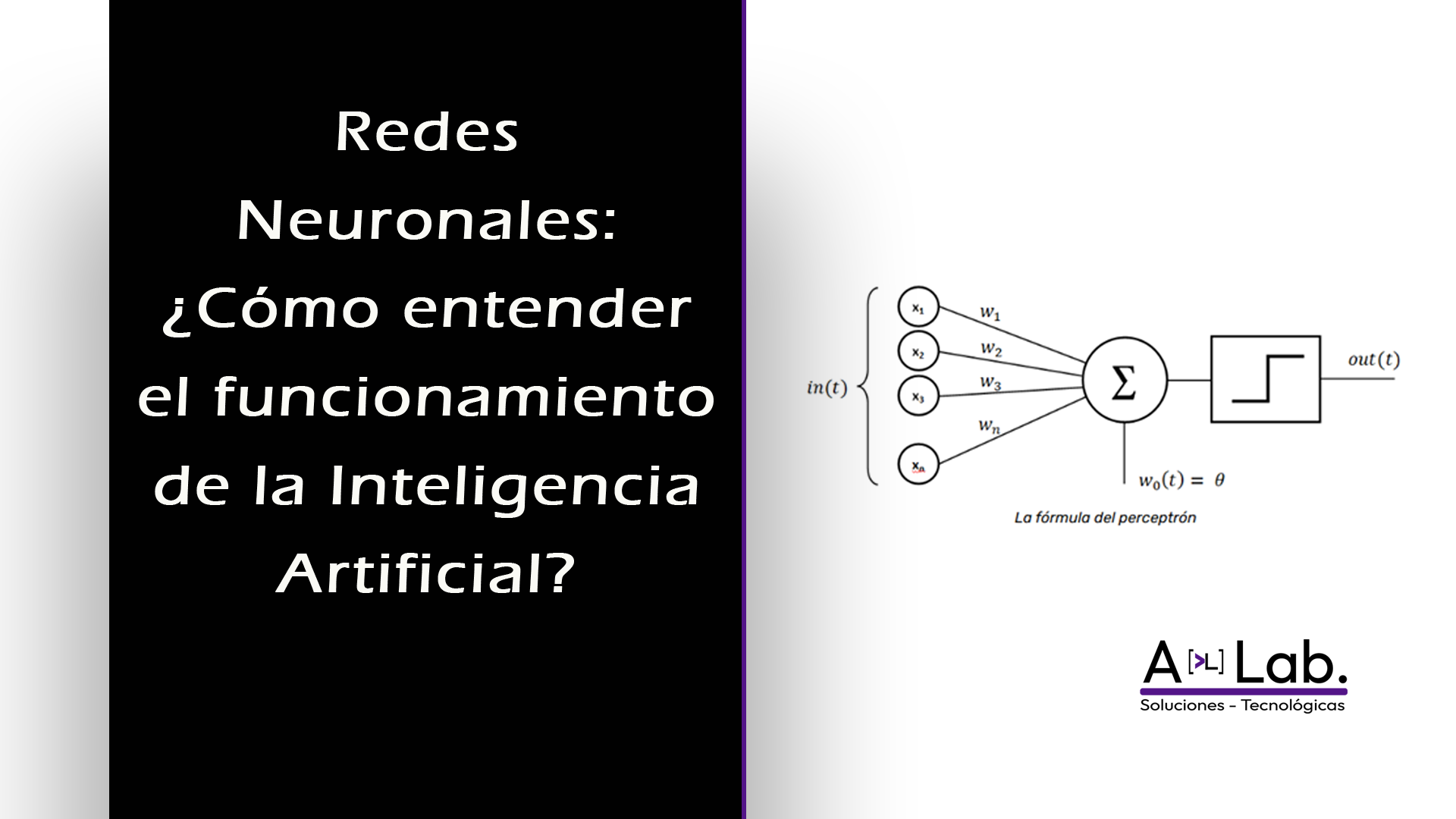
El Perceptrón: La neurona artificial
Inspirándose en este modelo, los científicos crearon la neurona artificial. En esencia, es una operación matemática que imita este proceso, y su versión más simple se llama Perceptrón.
Inventado en 1957 por Frank Rosenblatt, el Perceptrón es un clasificador binario (digamos, "sí" o "no"). Imagina que toma varias entradas (como características de una imagen), cada una con un "peso" (su importancia). La suma, aplica un "sesgo" (un umbral de activación, similar a un "Desde"), y si el resultado supera el límite, se "activa" mediante una función de activación.
Rosenblatt lo demostró con el Mark I Perceptron, entrenándolo para distinguir entre imágenes de hombres y mujeres. Los resultados fueron revolucionarios para la epoca, pero el modelo tenía una gran limitación: solo podía resolver problemas con soluciones lineales (como separar dos grupos con una línea recta). Si la distinción era más compleja, fallaba. Esta limitación es precisamente la que, años después, impulsaría el desarrollo de las redes neuronales profundas que conocemos hoy.
¿Cómo opera un perceptrón en la vida real? Ejemplo práctico para comprender
Imagina que eres un profesor y necesitas clasificar a tus alumnos para una feria de ciencias según su perfil: "científico" o "humanista". Te encuentras con un caso complicado:
- Pedro: 6,9 en Matemáticas y 6,5 en Filosofía.
- Agustín: 6,5 en Matemáticas y 6,9 en Filosofía.
Si aplicas un promedio simple, ambos tienen 6,7. ¡Es un empate! El promedio no logra captar la inclinación de cada estudiante. Aquí es donde un perceptrón puede ser mucho más inteligente.
La Fórmula del Perceptrón
Recordemos la fórmula que define a un perceptrón:
Z = (Entrada₁ × Peso₁) + (Entrada₂ × Peso₂) + Sesgo
Pero Z no es la respuesta final. La respuesta la da la Función de Activación. En nuestro caso, usaremos una simple función escalón:
- Si Z ≥ Umbral (11) → Clase 1 (Perfil Científico)
- Si Z < Umbral (11) → Clase 0 (Perfil Humanista)
Aplicando el Perceptrón a Pedro y Agustín
Digamos que, después de "entrenar" nuestro modelo con datos de años anteriores (un proceso clave del que hablaremos luego), el perceptrón aprendió los siguientes valores:
- Peso para Matemáticas (w₁): 1 (Tiene alta importancia para el perfil científico)
- Peso para Filosofía (w₂): 0,5 (Tiene importancia, pero menor)
- Sesgo (b): 1 (Un ajuste que ayuda a establecer el nivel de dificultad para ser clasificado como científico)
Ahora, calculemos:
Para Pedro:
Z = (6,9 × 1) + (6,5 × 0,5) + 1
Z = 6,9 + 3,25 + 1
Z = 11,15
Función de Activación: ¿11,15 ≥ 11? SÍ → Perfil Científico
Para Agustín:
Z = (6,5 × 1) + (6,9 × 0,5) + 1
Z = 6,5 + 3,45 + 1
Z = 10,95
Función de Activación: ¿10,95 ≥ 11? NO → Perfil Humanista
¿Funciona el Perceptron?
Como se puede apreciar el Perceptron ha logrado identificar y clasificar quien es el mejor alumno para asistir a la Feria Científica. Este ejemplo es simple y lineal y solo busca explicar de forma sencilla con el objetivo que cualquier persona lo pueda comprender.
Es importante mencionar que los valores de los pesos y el sesgo se establecen de forma arbitraria y estos son obtenidos del proceso de entrenamiento. Un perceptrón simple como este fue "entrenado" mostrándole muchos ejemplos de estudiantes ya clasificados, y mediante un algoritmo, ajustó automáticamente estos números hasta que pudo replicar las clasificaciones correctas. Esa capacidad de aprender de los datos es la esencia del aprendizaje automático.
¿Cómo el Perceptrón "Aprende"?: El Proceso de Entrenamiento
En el ejemplo anterior, usamos pesos (1, 0.5) y un sesgo (1) que parecían salir de la nada. La magia real del Perceptrón no es usar estos valores, sino descubrirlos por sí mismo a través de un proceso llamado entrenamiento.
Imaginemos que somos el profesor y tenemos datos históricos de 4 estudiantes del año pasado, donde ya sabemos con certeza su perfil. Esta será nuestra "verdad de terreno" o "dataset" de entrenamiento:
| Estudiante | Matemáticas (x₁) | Filosofía (x₂) | Perfil (target) |
|---|---|---|---|
| Ana | 7.5 | 5.0 | Científico (1) |
| Luis | 6.0 | 8.0 | Humanista (0) |
| María | 8.0 | 4.5 | Científico (1) |
| José | 5.5 | 7.5 | Humanista (0) |
Inicialización - Empezar en Cero
En esta etapa el Perceptron no sabe absolutamente nada si cuales son los pesos asociados a cada asignatura (matemática y filosofía) por lo que inicializamos con pesos y sesgo igual a 0 los cuales se irán ajustando a medida que se ejecute el Perceptron.
- Peso para Matemáticas (w₁) = 0
- Peso para Filosofía (w₂) = 0
- Sesgo (b) = 0
Paso 2: La Fórmula de Predicción y Activación
Utilizaremos la misma formula usada en el ejemplo de Pedro y Agustín, la que corresponde a un Perceptron Simple.
Z = (x₁ * w₁) + (x₂ * w₂) + b
Nuestra función de activación o umbral será el siguiente y es muy importante comprenderla ya que es la que nos permite definir si se cumple una condición de clasificación.
- Si Z ≥ 0 → Predice "Científico" (1)
- Si Z < 0 → Predice "Humanista" (0)
El Algoritmo de Aprendizaje - La Regla del Perceptrón
Una vez definidos los parámetros en el proceso de aprendizaje del Perceptron estableceremos las siguientes reglas:
- Debe calcular la predicción usando los pesos y sesgo actuales
- Una vez obtenido el resultado debe comparar con la verdad (target)
- Si se detecta un error, por ejemplo, que no se cumple con el target se deben actualizar los parámetros
Como ya conocemos cuales son las condiciones reales de un perfil científico si la predicción es DEMASIADO BAJA (debería ser 1 pero es 0) se debe aplicar el siguiente algoritmo para el ajuste:
nuevo_w₁ = w₁_actual + (tasa_aprendizaje * x₁)
nuevo_w₂ = w₂_actual + (tasa_aprendizaje * x₂)
nuevo_b = b_actual + tasa_aprendizaje
En el caso que la predicción es DEMASIADO ALTA (debería ser 0 pero es 1) para el perfil humanista se debe aplicar el siguiente algoritmo:
nuevo_w₁ = w₁_actual - (tasa_aprendizaje * x₁)
nuevo_w₂ = w₂_actual - (tasa_aprendizaje * x₂)
nuevo_b = b_actual - tasa_aprendizaje
Para definir nuestra tasa de aprendizaje iniciaremos con 0.1 que es un numero bajo y nos permitirá conocer cuál es la velocidad de aprendizaje de nuestro perceptrón.
Simulación del Entrenamiento - Primera Época
En el primer ejemplo analizaremos el caso de Ana:
Ejemplo 1: Ana (x₁=7.5, x₂=5.0, target=1)
Z = (7.5×0) + (5.0×0) + 0 = 0 → Predice 0 (Humanista) ❌ ERROR!
Actualización (predicción muy baja):
- w₁ = 0 + (0.1 × 7.5) = 0.75
- w₂ = 0 + (0.1 × 5.0) = 0.50
- b = 0 + 0.1 = 0.1
Ejemplo 2: Luis (x₁=6.0, x₂=8.0, target=0)
Z = (6.0×0.75) + (8.0×0.50) + 0.1 = 4.5 + 4.0 + 0.1 = 8.6 → Predice 1 (Científico) ❌ ERROR!
Actualización (predicción muy alta):
- w₁ = 0.75 - (0.1 × 6.0) = 0.15
- w₂ = 0.50 - (0.1 × 8.0) = -0.30
- b = 0.1 - 0.1 = 0
Ejemplo 3: María (x₁=8.0, x₂=4.5, target=1)
Z = (8.0×0.15) + (4.5×-0.30) + 0 = 1.2 - 1.35 + 0 = -0.15 → Predice 0 (Humanista) ❌ ERROR!
Actualización (predicción muy baja):
- w₁ = 0.15 + (0.1 × 8.0) = 0.95
- w₂ = -0.30 + (0.1 × 4.5) = 0.15
- b = 0 + 0.1 = 0.1
Ejemplo 4: José (x₁=5.5, x₂=7.5, target=0)
Z = (5.5×0.95) + (7.5×0.15) + 0.1 = 5.225 + 1.125 + 0.1 = 6.45 → Predice 1 (Científico) ❌ ERROR!
Actualización (predicción muy alta):
- w₁ = 0.95 - (0.1 × 5.5) = 0.40
- w₂ = 0.15 - (0.1 × 7.5) = -0.60
- b = 0.1 - 0.1 = 0
Resultados del Entrenamiento
Después de procesar los 4 ejemplos una vez (una "época"), nuestros parámetros son:
- w₁ (Matemáticas) = 0.40
- w₂ (Filosofía) = -0.60
- b (Sesgo) = 0
El perceptrón ha aprendido por sí mismo que:
- Las matemáticas tienen peso positivo (0.40) → contribuyen al perfil científico
- La filosofía tiene peso negativo (-0.60) → contribuye al perfil humanista
- El sesgo es neutral por ahora (0)
Verificación con Nuestros Casos Originales
Ahora probemos con Pedro y Agustín usando los pesos APRENDIDOS:
Para Pedro (Mat: 6.9, Fil: 6.5):
Z = (6.9 × 0.40) + (6.5 × -0.60) + 0 = 2.76 - 3.90 = -1.14
Como Z < 0 → Humanista ❌ (Esto no coincide con nuestro ejemplo anterior)
Para Agustín (Mat: 6.5, Fil: 6.9):
Z = (6.5 × 0.40) + (6.9 × -0.60) + 0 = 2.60 - 4.14 = -1.54
Como Z < 0 → Humanista ✅
¿Por qué falló con Pedro? ¡Porque necesitamos más entrenamiento! En la práctica, un Perceptrón necesita pasar por los datos de entrenamiento muchas veces (muchas épocas) hasta que los pesos converjan a valores que clasifiquen correctamente la mayoría de los ejemplos.
Es posible que hayas notado que en nuestro primer ejemplo con Pedro y Agustín utilizamos un umbral de 11, mientras que en el proceso de entrenamiento posterior usamos 0. Esta diferencia es intencionada y refleja una flexibilidad fundamental del perceptrón: el umbral puede ajustarse según las necesidades del problema. En la práctica, muchos modelos simplifican este aspecto utilizando un umbral de 0, ya que el sesgo (b) se encarga de absorber ese nivel de activación. Lo importante es comprender que tanto el umbral como el sesgo trabajan conjuntamente para establecer el punto de decisión, y durante el entrenamiento ambos valores se optimizan automáticamente.
Este proceso de:
- Predecir
- Calcular el error
- Ajustar pesos y sesgo
- Repetir
es la esencia del aprendizaje supervisado. Con suficientes iteraciones, el Perceptrón encontraría pesos como los que usamos intuitivamente en el primer ejemplo (w₁=1, w₂=0.5, b=1), que sí logran hacer la distinción correcta.
Aplicación del Perceptron en la Inteligencia Artificial
Entendiendo cómo opera un perceptrón, podemos entender como este es utilizado en la inteligencia artificial moderna.
Recordemos que el Perceptron es un modelo matemático que nos permite realizar clasificaciones binarias, las cuales deben ser claramente separables linealmente.
En AlchemyLab utilizamos estos principios fundamentales de las redes neuronales para desarrollar soluciones de IA personalizadas para empresas chilenas. Desde sistemas de clasificación de documentos hasta asistentes virtuales inteligentes, la comprensión de estos conceptos básicos nos permite crear herramientas que realmente entienden y se adaptan a las necesidades específicas de cada negocio.
¿Interesado en implementar soluciones de IA en tu empresa?
Visita www.alchemylab.cl y contáctanos para una asesoría personalizada.